[프로그래머스 스쿨][Python] 멀리 뛰기
2023. 2. 3. 11:39ㆍ알고리즘 문제풀이
반응형

문제
문제 설명
효진이는 멀리 뛰기를 연습하고 있습니다. 효진이는 한번에 1칸, 또는 2칸을 뛸 수 있습니다. 칸이 총 4개 있을 때,
- (1칸, 1칸, 1칸, 1칸)
- (1칸, 2칸, 1칸)
- (1칸, 1칸, 2칸)
- (2칸, 1칸, 1칸)
- (2칸, 2칸)
의 5가지 방법으로 맨 끝 칸에 도달할 수 있습니다. 멀리뛰기에 사용될 칸의 수 n이 주어질 때, 효진이가 끝에 도달하는 방법이 몇 가지인지 알아내, 여기에 1234567를 나눈 나머지를 리턴하는 함수, solution을 완성하세요. 예를 들어 4가 입력된다면, 5를 return하면 됩니다.
제한사항
- n은 1 이상, 2000 이하인 정수입니다.
입출력 예시
| n | result |
| 4 | 5 |
| 3 | 3 |
문제: 프로그래머스 스쿨 - 연습문제 - 멀리 뛰기
문제 풀이
유의사항
- 경우의 수 문제중에 가장 대표적인 문제 유형이다. (피보나치 수열)
- 점화식을 활용하여 문제를 해결할 수 있다.
- 재귀 함수, 반복문을 사용한 풀이 둘 다 가능하다.
- 재귀함수를 사용할 경우, 메모이제이션을 활용하지 않으면 n=2000이므로 시간 초과가 날 수 있다.
- 기하급수적으로 증가하는 수열이기에, 금새 표현가능한 수의 범위를 초과해 버린다.
(1234567로 나누어주는 것을 잊지 말자.)
풀이
- 핵심 아이디어: 점프는 1칸 혹은 2칸으로만 이루어지기에, n번째의 경우의 수는 (n-1)번째와 (n-2)번째에서의 점프의 합으로 이루어 진다.
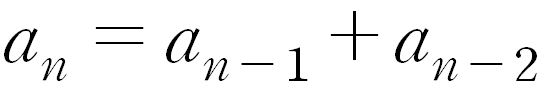
전체 코드
def solution(n):
answer = 0
a_n_1 = 2
a_n_2 = 1
if n==1: #재귀함수의 Base Case에 해당
return 1
if n==2:
return 2
for i in range(n-2):
answer = (a_n_1 + a_n_2) % 1234567
# 표현 가능한 수의 범위를 초과하지 않도록 나누어 준다.
a_n_2 = a_n_1
a_n_1 = answer
return answer
반응형
'알고리즘 문제풀이' 카테고리의 다른 글
| [프로그래머스 스쿨][Python] 다음 큰 숫자 (0) | 2023.02.07 |
|---|---|
| [프로그래머스 스쿨][Python] 숫자 블록 (조건 이상) (0) | 2023.02.03 |
| [프로그래머스 스쿨][Python] 가장 큰 정사각형 찾기 (1) | 2023.02.02 |
| [프로그래머스 스쿨][Python] 3 x n 타일링 (0) | 2023.01.31 |
| [프로그래머스 스쿨][Python] 124 나라의 숫자 (0) | 2023.01.31 |